Delphi - сбориник статей
Методы улучшения базового маршрута
Метод 2.1 (перестановок, Permutations). Совершается последовательный проход по парам соседних вершин всех звеньев с перестановкой этих вершин. Если перестановка уменьшает длину маршрута, то этот маршрут считается текущим. Производятся новые попытки улучшить его тем же методом до тех пор, пока перестановки не дадут эффекта. Далее аналогичным образом выполняются перестановки по трем соседним вершинам из числа тех, которые не попали в число ранее проведенных операций с двумя соседними вершинами (перестановки более широкого диапазона, т. е. по 4 и более, не выполнялись). Эксперименты с графами показали, что процедура улучшения маршрута при помощи перестановок достаточно эффективна и быстродействие ее весьма высоко.
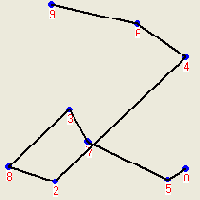
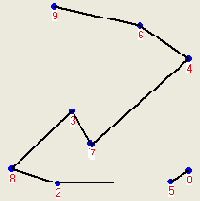
Метод 2.2 (удаление петлей, CrossDeleting). Часто текущий маршрут содержит петли. Например, на рисунке 1 цепочка вершин 5-7-3-8-2-4 образуют петлю. Петля начинается с левой по ходу маршрута вершины отрезка 5-7 и заканчивается правой вершиной отрезка 2-4. Существование петли определяется наличием пересекающихся отрезков маршрута. Если внутреннюю цепочку петли повернуть в противоположном направлении, то есть заменить указанную цепочку на 5-2-8-3-7-4, то петля исчезнет (рисунок 2), а маршрут станет короче. Метод отличается чрезвычайно высоким быстродействием и высокой эффективностью.
 |
 |
|
| Рисунок 1.Маршрут с петлей | Рисунок 2. Улучшенный маршрут |
Метод 2.3 (разворот цепочек, ChainTurnings). Как показали эксперименты, отсутствие петлей еще не означает, что процедура разворота цепочек без петлей неэффективна. Для оптимизации текущего маршрута применялась процедура разворота всех возможных цепочек. Метод имеет самое низкое быстродействие в сравнении с другими методами улучшения. Поэтому на практике его применяли для цепочек с числом звеньев не более шести.
Метод 2.4 (комбинированный, CorrectPath). После нахождения какого-нибудь базового маршрута G к нему применялась комбинированная процедура улучшения по методам 2.1 – 2.3. Хотя метод 2.2 является частным случаем метода 2.3, его все равно применяли из-за высокого быстродействия и способности к эффективному разворота цепочек из любого числа звеньев. Метод имеет код: procedure CorrectPath(N: Integer; var G: TIntVec; var Path: Integer); begin repeat until not Permutations(N,G) and not ChainTurnings(N,G) and not CrossDeleting(N,G) and not MoveTops(N,G); Path:= PathByG(N,G); // расчет длины маршрута end;